Blog Archives
Slope Stability Basics

The single biggest thing to know about slope stability, the breadth PE, is the factor of safety numbers:
1.5 – Permanent conditions
2.0 – Slope is supporting a building foundation
1.3 – temporary slope conditions
These will probably be in a word problem.
What is the factor of safety?
The factor of safety is a ratio of how stable the slope is given soil characteristics and geometry of the slope (angle and height etc).
The methods of determining the factor of safety for slope stability are somewhat advanced. I think they will definitely appear on the depth exam but likely not on the breadth. I suggest knowing they exist and where they are (Ch 210 Goswami, 40-7 CERM).
What Causes Slope Failure?
All of these things cause failure, eventually:
- Steepening of slopes
- Increase in groundwater pressure
- Weathering (which may be related to steepness)
- Vibrations, especially repetitive vibrations (traffic), or extreme vibrations (earthquakes)
- Extra Loading above the slope
- Excavation at the toe of the slope
What prevents Slope Failure?
- Making it less steep through grading
- Retaining structures
- Weight at the tow
- Less weight above the slope
- Reduce or remove vibrations
- basically reverse the causes….
Soil Permeability
Soil permeability is a measure of fluids flowing through the soil. Aside from the soil, ease of flow also depends on the fluid (oil is slower than water etc) but you only need to worry about the soil end of things for the geotech breadth.
Coefficient of Permeability (K)
The coefficient of permeability is the characteristic that measures how permeable a soil is. The units of K are the same as velocity (ft/s), but theoretically it is volume per area per time ($$\frac{ft^3}{ft^2 t}$$).
Typical values for K are probably in your reference of choice, and probably also in any permeability problem prompts. In the CERM the values are on page 21-3 and are provided for many different unit types.
Darcy’s Law
Darcy’s Law will calculate the groundwater flow (Q) through a soil given a hydraulic conductivity (K) a hydraulic grade (i, units are $$\frac{in}{in}$$ or $$\frac{ft}{mi}$$ etc.) and an area covered (A). The units of area should match the units for grade.
$$ Q = -KiA$$
Some references show the negative sign, others don’t. I think this is to account for the hydraulic grade and direction of flow. In most cases the point you are measuring the flow at is roughly the lowest point in the area (A). The water table grade/slope from any other point will be negative to end at the point, so to make the flow positive they throw that negative in to reverse the grade negative. Anyway, regardless of the negative, the absolute value for flow doesn’t change and you should be able to tell what direction the flow is going in.
Soil Classification
There are two main methods of soil classification: AASHTO, and the Unified Soil Classificaiton System (USCS). Both methods involve finding the appropriate soil class given some parameters like passing a certain sieve size, liquid limit, plastic limit, significant makeup, and other ratings.
AASHTO classification returns an A-1 through A-8 rating. A-1 is the best all-round and A-8 is not really suitable for building.
USCS classification returns a two-digit group symbol for the soil such as GW for gravelly well-graded, SM for silty sand, CL for low plasticity clay etc.
You will need to be familiar with the sieve sizes (e.g. #200 allows up to 0.075 mm grains to pass) and how to determine what percent of the soil passes through that sieve, find the charts for this in your reference.
The Plasticity Index (PI) is equal to the Liquid Limit (LL) minus the Plastic Limit (PL):
$$ PI = LL – PL $$ Click here to continue reading
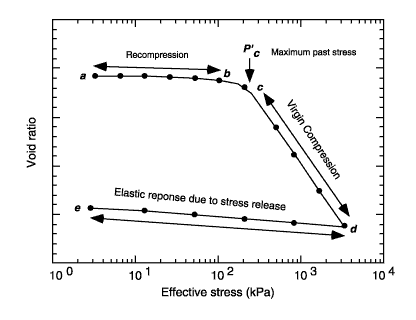
Soil Mechanics – Consolidation
Consolidation is a form of settlement where the air and liquids in a soil (the voids) are removed due to pressures acting on the soil. Consolidation can occur over a long period of time and can destroy structures if not address soon enough.
The distance of consolidation is determined using this equation:
$$ s = H \varepsilon_v = \frac{H \Delta e}{1 + e_0} $$
Where:
s = settlement
H = layer thickness
\(e_0\) = initial void ratio
\(Delta e\) = change of the void ratio due to the increase in vertical stress at the midpoint of the layer