Soil Mechanics – Consolidation
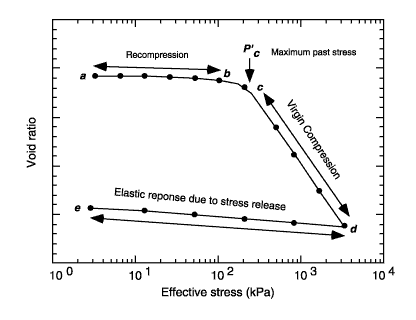
Consolidation is a form of settlement where the air and liquids in a soil (the voids) are removed due to pressures acting on the soil. Consolidation can occur over a long period of time and can destroy structures if not address soon enough.
The distance of consolidation is determined using this equation:
$$ s = H \varepsilon_v = \frac{H \Delta e}{1 + e_0} $$
Where:
s = settlement
H = layer thickness
\(e_0\) = initial void ratio
\(Delta e\) = change of the void ratio due to the increase in vertical stress at the midpoint of the layer
LRFD Load Combinations
Choose the combination that results in the highest U, use U in your calculations.
$$U = 1.4(D+F)$$
$$U = 1.2(D+F+T) + 1.6(L+H) + 0.5(L_r or S or R)$$
$$ U = 1.2D + 1.6(L_r or S or R) + (1.0L or 0.8W)$$
$$ U = 1.2D + 1.6W + 1.0L + 0.5(L_r or S or R)$$
$$ U = 1.2DL + 1.0E + 1.0L + 0.2S$$
$$U = 0.9D + (1.6W or 1.0E) + 1.6H$$
D = Dead Load, L = Live Load, T = self-straining, H = earth pressure, \(L_r\) = roof live load, S = Snow Load, R = rain load, E = earthquake load
Dead Loads and Live Loads
Structural loads are placed into two main categories, dead loads and live loads.
Dead loads are loads on a structure due to the structure’s own weight.
Live loads are loads on the structure due to objects that are not permanent like people, furniture, and vehicles.
The goal of structural design is to accurately tally up the projected loads in a structure, convert them to stress, and compare that stress to what the structure can handle (the designed strength). There are two camps on how this is to be done:
Shear and Bending Stresses in Beams
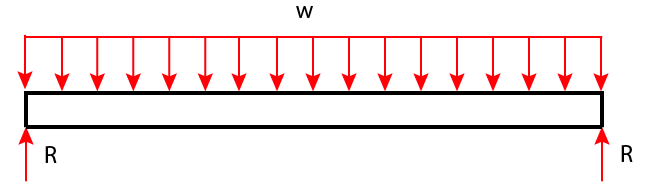
Beams are one of the main design elements a structural engineer will work with. This is a loaded simply supported beam:
For the PE exam, a loaded beam has two main options for failure, shear and bending.